题目内容
13.先化简,再求值:$(\frac{x+2}{{{x^2}-2x}}-\frac{x-1}{{{x^2}-4x+4}})÷\frac{x-4}{x}$,其中x满足x2-4x+1=0.分析 先根据分式混合运算的法则把原式进行化简,再根据题意得出x2-4x=-1,代入进行计算即可.
解答 解:原式=[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{{(x-2)}^{2}}$]•$\frac{x}{x-4}$
=$\frac{{x}^{2}-4-{x}^{2}+x}{x{(x-2)}^{2}}$•$\frac{x}{x-4}$
=$\frac{x-4}{x{(x-2)}^{2}}$•$\frac{x}{x-4}$
=$\frac{1}{{(x-2)}^{2}}$
=$\frac{1}{{x}^{2}-4x+4}$,
∵x2-4x+1=0,
∴x2-4x=-1,
∴原式=$\frac{1}{-1+4}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
3.将二次函数y=x2+1的图象向右平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2 | B. | y=(x-1)2 | C. | y=(x-1)2+1 | D. | y=(x+1)2+1 |
4.下列命题:
①圆上任意两点间的部分叫弧
②圆心角相等则它们所对的弧相等
③等弧的所对的弦相等
④直径是圆的对称轴
⑤顶点在圆上,两边和圆相交的角是圆周角.
其中正确的有( )个.
①圆上任意两点间的部分叫弧
②圆心角相等则它们所对的弧相等
③等弧的所对的弦相等
④直径是圆的对称轴
⑤顶点在圆上,两边和圆相交的角是圆周角.
其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
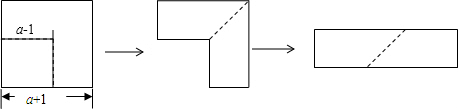

| A. | 2 cm2 | B. | 2a cm2 | C. | 4a cm2 | D. | (a2-1)cm2 |
5.小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了$\frac{1}{4}$,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
| A. | $\frac{40}{x+20}$=$\frac{3}{4}$×$\frac{40}{x}$ | B. | $\frac{40}{x}$=$\frac{3}{4}×\frac{40}{x+20}$ | C. | $\frac{40}{x+20}$+$\frac{1}{4}$=$\frac{40}{x}$ | D. | $\frac{40}{x}$=$\frac{40}{x+2}$-$\frac{1}{4}$ |
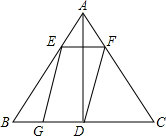 如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.
如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.