题目内容
13.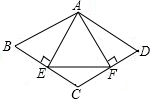 如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
分析 ①由等边三角形的性质得出∠EAF=60°,AE=AF,求出∠C=120°,由平行四边形的性质得出AB∥CD,∠C=∠BAD=120°,得出∠B=180°-∠C=60°,①正确;
②由平行四边形的性质得出∠D=∠B=60°,求出∠BAE=∠DAF=30°,得出∠EAF=120°-30°-30°=60°,但是AE不一定等于AF,②错误;
③由平行四边形的面积得出$\frac{1}{2}$BC•AE=$\frac{1}{2}$CD•AF,得出BC=CD,证出平行四边形ABCD是菱形,③正确;
④由菱形的性质得出BC=CD,由面积得出$\frac{1}{2}$BC•AE=$\frac{1}{2}$CD•AF,得出AE=AF,④正确;即可得出结论.
解答 解:①∵△AEF是等边三角形,
∴∠EAF=60°,AE=AF,
又∵AE⊥BC,AF⊥CD,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,
∴∠BAE=∠DAF=90°-60°=30°,
∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则$\frac{1}{2}$BC•AE=$\frac{1}{2}$CD•AF,
∴BC=CD,
∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,
则BC=CD,
∴$\frac{1}{2}$BC•AE=$\frac{1}{2}$CD•AF,
∴AE=AF,故④正确;
故答案为:①③④.
点评 本题考查了平行四边形的性质、等边三角形的判定与性质,菱形的判定与性质;熟练掌握等边三角形和菱形的判定与性质是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
11.不等式5x-1>2x+5的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
18.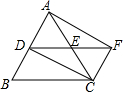 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE到F,使得EF=DE,那么四边形ADCF是( )
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE到F,使得EF=DE,那么四边形ADCF是( )
 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE到F,使得EF=DE,那么四边形ADCF是( )
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE到F,使得EF=DE,那么四边形ADCF是( )| A. | 等腰梯形 | B. | 直角梯形 | C. | 矩形 | D. | 菱形 |
5.在一个不透明的袋子装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
(2)当(1)中的m=2时,请直接写出事件A发生的概率.
(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2或3 |
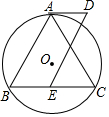 如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.
如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.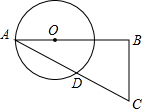 如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,
如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,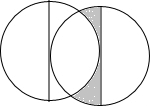 半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.