题目内容
20.如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )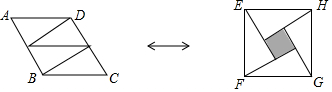
| A. | 1 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
分析 设直角三角形的长直角边为a,短直角边为b,于是得到2a=AD,根据直角三角形的性质得到∠A=60°,求得b=$\sqrt{3}$a于是得到S菱形ABCD=2ab=2$\sqrt{3}$a2,正方形EFGH面积=(2a)2=4a2,即可得到结论.
解答 解:设直角三角形的长直角边为b,短直角边为a,
∵四边形ABCD是菱形,
∴AD=AB,
即2a=AD,
∴∠A=60°,
∴b=$\sqrt{3}$a
∴S菱形ABCD=2ab=2$\sqrt{3}$a2,正方形EFGH面积=(2a)2=4a2,
∴菱形ABCD面积和正方形EFGH面积之比=$\frac{2\sqrt{3}{a}^{2}}{4{a}^{2}}$=$\frac{\sqrt{3}}{2}$,
故选C.
点评 本题考查了正方形的性质,直角三角形的性质,正确的理解题意是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.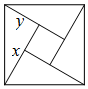 如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )
如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )
 如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )
如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )| A. | x2+y2=49 | B. | x-y=2 | C. | 2xy+4=49 | D. | x+y=13 |
5.在一个不透明的袋子装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
(2)当(1)中的m=2时,请直接写出事件A发生的概率.
(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2或3 |
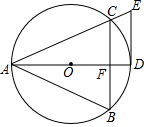 如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E.
如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E. 如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.
如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.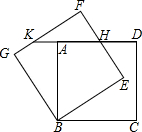 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则HD的长为$\sqrt{3}$-1.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则HD的长为$\sqrt{3}$-1.