题目内容
6.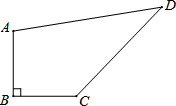 如图,四边形ABCD中,∠B=90°,AB=BC=3$\sqrt{2}$,CD=8,AD=10.
如图,四边形ABCD中,∠B=90°,AB=BC=3$\sqrt{2}$,CD=8,AD=10.(1)求∠BCD的度数.
(2)求四边形ABCD的面积.
分析 (1)连接AC,在直角三角形ABC中,利用勾股定理求出AC的长,再由CD与AD的长,利用勾股定理的逆定理判断得到三角形ACD为直角三角形,再由等腰直角三角形的性质,根据∠BCD=∠ACB+∠ACD即可求出;
(2)四边形ABCD面积=三角形ABC面积+三角形ACD面积,求出即可.
解答 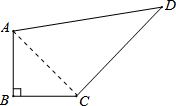 解:(1)连接AC,
解:(1)连接AC,
在Rt△ABC中,∠B=90°,AB=BC=3$\sqrt{2}$,
根据勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=6,∠ACB=45°,
∵CD=8,AD=10,
∴AD2=AC2+CD2,
∴△ACD为直角三角形,即∠ACD=90°,
则∠BCD=∠ACB+∠ACD=135°;
(2)根据题意得:S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×3$\sqrt{2}$×3$\sqrt{2}$+$\frac{1}{2}$×6×8=9+24=33.
点评 此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
11.不等式5x-1>2x+5的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
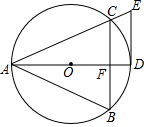 如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E.
如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E.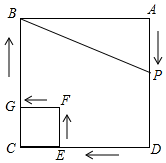 如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.
如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.