题目内容
17.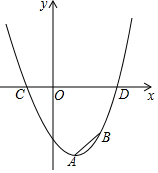 二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.
二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.(1)求A,B两点的坐标及二次函数的解析式;
(2)用配方法求该抛物线与x轴的两个交点坐标;
(3)如果M为x轴上一点,N为y轴上一点,以点A、B、M、N为顶点的四边形是平行四边形,求直线MN的函数表达式.
(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象,请你结合新图象回答,当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
分析 (1)如图1中,作AE⊥OD于E,BF⊥AE于F.设A(m,m2-2m-c),在Rt△ABF中,可得BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=1,推出B(m+1,m2-2m-c+1),把B点坐标代入y=x2-2x-c 得到m2-2m-c+1=(m+1)2-2(m+1)-c,解得m=1,即可解决问题.
(2)利用配方法解方程即可.
(3)如图2中,易知当M(1,0),N(0,-1)或M1(-1,0),N1(0,1)时,以点A、B、M、N为顶点的四边形是平行四边形
(4)如图3中,画出翻转后新的函数图象,由直线y=x+n确定出直线移动的范围,求出b的取值范围.
解答 解:(1)如图1中,作AE⊥OD于E,BF⊥AE于F.设A(m,m2-2m-c),
在Rt△ABF中,∵AB=$\sqrt{2}$,AF=1,
∴BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=1,
∴B(m+1,m2-2m-c+1),
把B点坐标代入y=x2-2x-c 得到m2-2m-c+1=(m+1)2-2(m+1)-c,
解得m=1,
∴A(1,-4),B(2,-3),
把A(1,-4)代入y=x2-2x-c 得到c=3,
∴二次函数的解析式为y=x2-2x-3.
(2)对于抛物线y=x2-2x-3,令y=0,得到x2-2x-3=0,
∵x2-2x=3,
∴(x-1)2=4,
∴x-1=±2,
∴x=-1或3,
∴C(-1,0),D(3,0).
(3)如图2中,
易知当M(1,0),N(0,-1)或M1(-1,0),N1(0,1)时,以点A、B、M、N为顶点的四边形是平行四边形
∴直线MN的解析式为y=x+1或y=x-1.
(4)如图4中,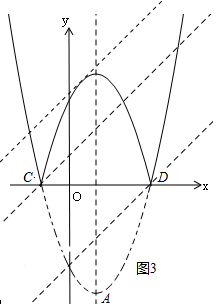
当直线y=x+n过点D时,把D(3,0)代入得:3+n=0,
n=-3,
当直线y=x+n过点C时,把C(-1,0)代入得:-1+n=0,
n=1,
∴当,b的取值范围是-3<n<1,
当直线y=x+n与翻折后的抛物线y=-(x-1)2+4只有一个公共点时,
$\left\{\begin{array}{l}{y=x+n}\\{y=-(x-1)^{2}+4}\end{array}\right.$,消去y得到x2-x+n-3=0,
由题意△=0,可得n=$\frac{13}{4}$,
观察图象可知,n>$\frac{13}{4}$时,直线y=x+n与此图象有两个公共点,
综上所述,当-3<n<1或n>$\frac{13}{4}$时,直线y=x+n与此图象有两个公共点.
点评 本题主要考查了二次函数的综合题,一次函数的应用、平行四边形的判定和性质、勾股定理,一元二次方程的根的判别式等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,学会寻找特殊点解决问题,属于中考压轴题.

 期末集结号系列答案
期末集结号系列答案(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2或3 |
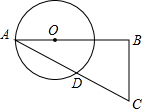 如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,
如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,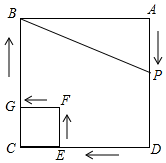 如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.
如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t. 如图,在?ABCD中,AB=3,BC=4,对角线AC,BD交于点O,点E为边AB的中点,连结OE,则OE的长为2.
如图,在?ABCD中,AB=3,BC=4,对角线AC,BD交于点O,点E为边AB的中点,连结OE,则OE的长为2.