题目内容
3. 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\sqrt{3}$ |
分析 连接OB、OC,证明△OBC是等边三角形,得出BC=OB=2,由垂径定理求出BM,再由勾股定理求出OM即可.
解答 解:连接OB、OC,如图所示:
则∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=2,
∵OM⊥BC,
∴BM=CM=$\frac{1}{2}$BC=1,
∴OM=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故选:D.
点评 本题考查了正多边形和圆、正六边形的性质、垂径定理、勾股定理、等边三角形的判定与性质;熟练掌握正六边形的性质,证明三角形是等边三角形和运用垂径定理求出BM是解决问题的关键.

练习册系列答案
相关题目
13.已知⊙O1的半径为3,⊙O2的半径长r(r>0),如果O1O2=3,那么⊙O1与⊙O2不可能存在的位置关系是( )
| A. | 两圆内含 | B. | 两圆内切 | C. | 两圆相交 | D. | 两圆外切 |
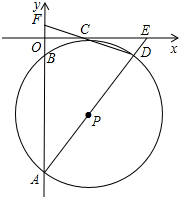 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).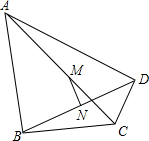 已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.
已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.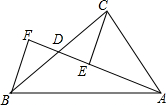 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )