题目内容
8.已知等腰三角形的周长等于20,底边为x,那么它的腰长y与x的函数关系式是y=-$\frac{1}{2}$x+10,x的取值范围是0<x<10.分析 等腰三角形的腰长=(周长-底边长)÷2,根据腰长大于0可得x的取值范围.
解答 解:腰长y与x的函数关系式是y=$\frac{20-x}{2}$=-$\frac{1}{2}$x+10,
由题意得:$\left\{\begin{array}{l}{-\frac{1}{2}x+10>0}\\{20-x>x}\end{array}\right.$,
解得:x<10
则x的取值范围是0<x<10.
故答案为:y=-$\frac{1}{2}$x+10,0<x<10.
点评 考查了一次函数关系式;根据腰长的代数式得到底边长的取值范围是解决本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某同学用描点法y=ax2+bx+c的图象时,列出了表:
由于粗心,他算错了其中一个y值,则这个错误的y值是-5.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
3. 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\sqrt{3}$ |
13.如果4a=5b(ab≠0),那么下列比例式变形正确的是( )
| A. | $\frac{5}{a}=\frac{4}{b}$ | B. | $\frac{a}{4}=\frac{b}{5}$ | C. | $\frac{a}{b}=\frac{4}{5}$ | D. | $\frac{4}{a}=\frac{b}{5}$ |
20. 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:
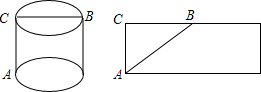
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A-C-B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A-C-B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
| A. | 楠楠同学正确,他的理论依据是“直线段最短” | |
| B. | 浩浩同学正确,他的理论依据是“两点确定一条直线” | |
| C. | 楠楠同学正确,他的理论依据是“垂线段最短” | |
| D. | 浩浩同学正确,他的理论依据是“两点之间,线段最短” |
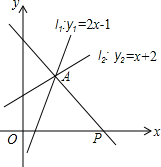 如图,直线l1:y1=2x-1与直线l2:y2=x+2相交于点A,点P是x轴上任意一点,直线l3是经过点A和点P的一条直线.
如图,直线l1:y1=2x-1与直线l2:y2=x+2相交于点A,点P是x轴上任意一点,直线l3是经过点A和点P的一条直线.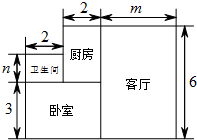 小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题: