题目内容
18.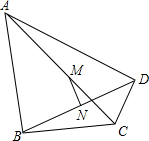 已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.
已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.(1)求证:MN⊥BD;
(2)在边AD上能否找到一点P,使得PB=PD?请说明理由.
分析 (1)连接BM、CM,根据在直角三角形中,斜边上的中线等于斜边的一半得到BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,根据等腰三角形的三线合一得到答案;
(2)根据线段垂直平分线的性质作图即可.
解答 解:(1)连接BM、CM,
∵∠ABC=∠ADC=90°,M是AC的中点,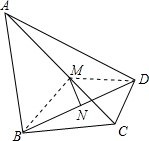
∴BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,
∴BM=DM,又N为BD的中点,
∴MN⊥BD;
(2)作线段BD的垂直平分线交AD于P,
根据线段垂直平分线上的点与线段两个端点的距离相等可知,
PB=PD.
点评 本题考查的是直角三角形的性质和等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3. 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
 如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O半径为2,则六边形的边心距OM的长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\sqrt{3}$ |
 根据下列语句画出图形:
根据下列语句画出图形: 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n), 如图,扇形AOB的面积,占圆O面积的15%,则扇形AOB的圆心角的度数是54°.
如图,扇形AOB的面积,占圆O面积的15%,则扇形AOB的圆心角的度数是54°.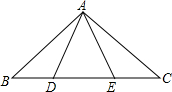 已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.
已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.