题目内容
2.计算:(1)$\frac{co{s}^{2}30°+co{s}^{2}60°}{tan60°•cos30°}$+tan60°
(2)2cos45°•sin45°-2sin30°•tan45°+$\sqrt{6}$•tan60°.
分析 (1)将特殊角的三角函数值代入后进行化简求值即可;
(2)将特殊角的三角函数值代入,然后化简二次根式,最后合并同类项即可.
解答 解:(1)原式=$\frac{(\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}{\sqrt{3}×\frac{\sqrt{3}}{2}}$+$\sqrt{3}$=$\frac{2}{3}$+$\sqrt{3}$;
(2)原式=2×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$-2×$\frac{1}{2}$×1+$\sqrt{6}$×$\sqrt{3}$=1-1+3$\sqrt{2}$=3$\sqrt{2}$.
点评 本题考查了特殊角的三角函数值.应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.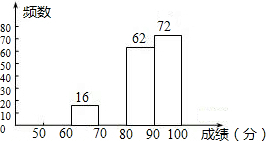 某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计
某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计
请你根据不完整的表格,回答下列问题:
(1)请直接写出m,a,b,c的值;
(2)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”?
 某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计
某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.02 |
| 80≤x<90 | 62 | c |
| 90≤x<100 | 72 | 0.36 |
(1)请直接写出m,a,b,c的值;
(2)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”?
17.下列二次根式中与其他三个不是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{98}$ | C. | $\sqrt{50}$ | D. | $\sqrt{48}$ |
12.一元一次不等式-x-2<1-2x的正整数解有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |