题目内容
5.观察下列一组按规律排列的数,用含n(n为正整数)的式子表示第n个数为$\frac{2n-1}{{2}^{n+2}}$$\frac{1}{8}$ $\frac{3}{16}$ $\frac{5}{32}$ $\frac{7}{64}$ …
分析 根据已知数字得出其分子与分母变化规律,进而得出答案.
解答 解:∵分子为1,3,5,7是连续奇数,则第n个式子的分子为2n-1,
分母为8=23,16=24,32=25,64=26,则第n个式子的分母为2n+2,
∴用含n(n为正整数)的式子表示第n个数为$\frac{2n-1}{{2}^{n+2}}$.
故答案为:$\frac{2n-1}{{2}^{n+2}}$.
点评 此题主要考查了数字变化规律,得出分子与分母的变化规律是解题关键.

练习册系列答案
相关题目
15.以下列长度的线段为边不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 6,24,25 |
16.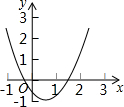 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
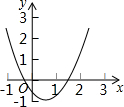 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
17.大于-3而不大于3的所有整数的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14. 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |




 化简:
化简: