Question

15．在Rt△ABC中，∠C=90°，AB=10$\sqrt{3}$，cos∠ABC=$\frac{3}{5}$，D是AC上一点，且∠DBC=30°，求BC、AD的长．

Answer 1

分析 首先根据题意画出图形，然后根据余弦定理计算出BC的长，再利用勾股定理可计算出AC的长，再次利用特殊角的三角函数值计算出CD的长，再根据线段的和差关系可得AD长．

解答 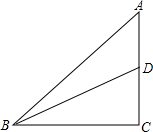解：如图，∵cos∠ABC=$\frac{3}{5}$，∠C=90°，
∴$\frac{BC}{AB}$=$\frac{3}{5}$，
∵AB=10$\sqrt{3}$，
∴BC=10$\sqrt{3}$×$\frac{3}{5}$=6$\sqrt{3}$，
∴AC=$\sqrt{A{B}^{2}-C{B}^{2}}$=8$\sqrt{3}$，
∵∠DBC=30°，
∴CD=BC•tan30°=6$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=6，
∴AD=AC-CD=8$\sqrt{3}$-6．

点评 此题主要考查了解直角三角形，关键是掌握特殊角的三角函数值，以及勾股定理的应用．