Question

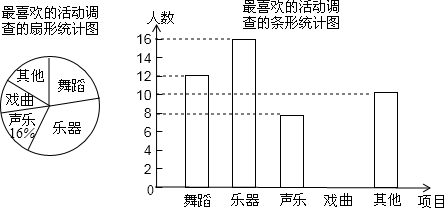
6．为了解学生的艺术特长发展情况，某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中，你最喜欢哪一项活动（每人只限一项）的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制如下两幅不完整的统计图．请你根据统计图解答下列问题：
（1）在这次调查中，一共抽查了50名学生，其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为24%．扇形统计图中喜欢“戏曲”部分扇形的圆心角为28.8度．
（2）请你补全条形统计图．
（3）若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率．

Answer 1

分析 （1）用喜欢声乐的人数除以所占的百分比，进行计算即可得解；用喜欢舞蹈的人数除以被抽查的总人数即可；求出喜欢戏曲的人数，用戏曲人数所占比例乘以360°可得；
（2）由（1）中求得的戏曲人数，补全统计图即可；
（3）画出树状图，然后根据概率公式列式进行计算即可得解

解答 解：（1）一共抽查学生数为：8÷16%=50，
“舞蹈”活动项目的人数占抽查总人数的百分比为：$\frac{12}{50}$×100%=24%；
∵喜欢戏曲的人数：50-12-16-8-10=50-46=4人，
∴扇形统计图中喜欢“戏曲”部分扇形的圆心角为：$\frac{4}{50}$×360°=28.8°，
故答案为：50，24%，28.8．

（2）补全统计图如图：


（3）画树状图如下：

∵共有12种等可能结果，其中恰好选中“舞蹈、声乐”这两项活动的有2种结果，
故恰好选中“舞蹈、声乐”两项活动的概率是：$\frac{2}{12}$=$\frac{1}{6}$．

点评 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．