题目内容
18. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )| A. | 140米 | B. | 150米 | C. | 160米 | D. | 240米 |
分析 多边形的外角和为360°每一个外角都为24°,依此可求边数,再求多边形的周长.
解答 解:∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走了:15×10=150米.
故选B.
点评 本题考查多边形的内角和计算公式,多边形的外角和.关键是根据多边形的外角和及每一个外角都为24°求边数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.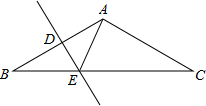 如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
 如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
如图所示,底边BC为2$\sqrt{3}$,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )| A. | 2+2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 4 | D. | 3$\sqrt{3}$ |
10. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7. 如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )
如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )
 如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )
如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )| A. | 18° | B. | 36° | C. | 45° | D. | 54° |
 如图,已知一次函数y=kx+b的图象经过点A(2,1),且y的值随着x的值增大而减小,当函数值y≥1时,那么x的取值范围是x≤2.
如图,已知一次函数y=kx+b的图象经过点A(2,1),且y的值随着x的值增大而减小,当函数值y≥1时,那么x的取值范围是x≤2.
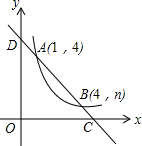 如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
如图,直线y=ax+b与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点. 如图,在⊙O中,∠AOB+∠COD=70°,AD与BC交于点E,则∠AEB的度数为35°.
如图,在⊙O中,∠AOB+∠COD=70°,AD与BC交于点E,则∠AEB的度数为35°.