题目内容
17．
如图点A、B、C在⊙O上，CO延长线交AB于点D，∠A=60°，∠B=30°，则∠ADC的度数为90°．
分析 根据圆周角定理求得∠BOC=120°，进而根据三角形的外角的性质求得∠BDC=90°，然后根据邻补角求得∠ADC的度数．
解答 解：∵∠A=60°，
∴∠BOC=2∠A=120°，
∵∠B=30°，∠BOC=∠B+∠BDC，
∴∠BDC=∠BOC-∠B=120°-30°=90°，
∴∠ADC=180°-∠BDC=90°，
故答案为：90°．
点评 本题考查了圆心角和圆周角的关系及三角形外角的性质，圆心角和圆周角的关系是解题的关键．
练习册系列答案
相关题目
7．
如图，AB∥CD，CE平分∠BCD，∠B=36°，则∠DCE等于（ ）
如图，AB∥CD，CE平分∠BCD，∠B=36°，则∠DCE等于（ ）| A． | 18° | B． | 36° | C． | 45° | D． | 54° |
如图，在正六边形ABCDEF中，连接AD，AE，则∠DAE=30°．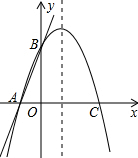
如图，已知直线y=3x+3与x轴交于点A，与y轴交于点B，过A，B两点的抛物线交x轴于另一点C（3，0）．
如图，在⊙O中，∠AOB+∠COD=70°，AD与BC交于点E，则∠AEB的度数为35°．