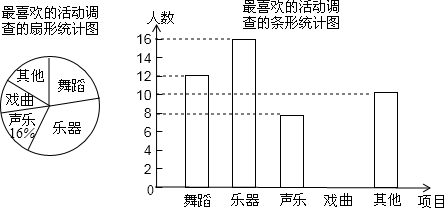
已知点C是AB的黄金分割点.AC=4.则BC的长2$\sqrt{5}$+2．题目和参考答案——青夏教育精英家教网—

题目内容

16．已知点C是AB的黄金分割点（AC＜BC），AC=4，则BC的长2$\sqrt{5}$+2．

分析把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（$\frac{\sqrt{5}-1}{2}$）叫做黄金比．

解答解：由题意知：AC=$\frac{\sqrt{5}-1}{2}$AB，AC=4，
可得：AB=$4÷\frac{\sqrt{5}-1}{2}=2\sqrt{5}+2$．
故答案为：2$\sqrt{5}$+2．

点评考查了黄金分割点的概念，关键是能够根据黄金比进行计算．

练习册系列答案

相关题目

6．

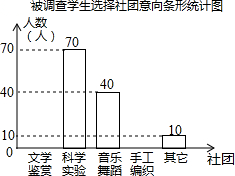为深化课程改革，浠水思源实验学校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：
浠水思源实验学校被调查学生选择社团意向统计表

选择意向	文学鉴赏	科学实验	音乐舞蹈	手工编织	其他
所占百分比	a	35%	b	10%	c

根据统计图表中的信息，解答下列问题：
（1）求本次调查的学生总人数及a，b，c的值．
（2）将条形统计图补充完整．
（3）若该校共有3400名学生，试估计全校选择“科学实验”社团的学生人数．

7．

如图，ABCD为正方形，O为对角线AC、BD的交点，则△COD绕点O经过下列哪种旋转可以得到△DOA（　　）

4．在|-3|，3⁰，3^-2，$\sqrt{3}$这四个数中，最大的数是（　　）

3⁰

3^-2

11．

如图所示，AB∥CD，AF与CD交于点E，BE⊥AF，∠B=65°，则∠DEF的度数是
（　　）

1．如图，已知二次函数y=-x²+bx+c（b，c为常数）的图象经过点A（3，1），点C（0，4），顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BC．
（1）求该二次函数的解析式及点M的坐标；
（2）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；
（3）点P是直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似，请直接写出所有点P的坐标（直接写出结果，不必写解答过程）．

8．

如图，已知一次函数y=kx+b的图象经过点A（2，1），且y的值随着x的值增大而减小，当函数值y≥1时，那么x的取值范围是x≤2．

5．先化简，再求值：$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$×（$\frac{1}{b}$-$\frac{1}{a}$）-$\frac{1}{a}$，其中a=b=2016．

6．为了解学生的艺术特长发展情况，某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中，你最喜欢哪一项活动（每人只限一项）的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制如下两幅不完整的统计图．请你根据统计图解答下列问题：
（1）在这次调查中，一共抽查了50名学生，其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为24%．扇形统计图中喜欢“戏曲”部分扇形的圆心角为28.8度．
（2）请你补全条形统计图．
（3）若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率．

试题分类