题目内容
 已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.
已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.(1)若点P到点A、点B的距离相等,则点P对应的数x=
(2)当x=
(3)当点P以每分钟1个单位长度的速度从A点向左运动时,同时点Q以每分钟3个单位长度从点B向左运动,几分钟后P、Q两点之间的距离为8?此时P、Q两点表示的数分别是多少?
考点:一元一次方程的应用,数轴
专题:
分析:(1)根据中点坐标公式即可得到点P对应的数x;
(2)利用当P在A左侧时,当P在B右侧时,分别得出即可;
(3)可设y分钟后P、Q两点之间的距离为8,根据P、Q两点之间的距离为8列出方程求解即可.
(2)利用当P在A左侧时,当P在B右侧时,分别得出即可;
(3)可设y分钟后P、Q两点之间的距离为8,根据P、Q两点之间的距离为8列出方程求解即可.
解答:解:(1)点P对应的数x=([9+(-3)]÷2=3.
(2)设点P表示的数为x,则|x+3|+|x-9|=15
当x≤-3时,原方程可化为:-x-3+9-x=15,解得x=-4.5;
当-3<x<9时,原方程可化为:x+3+9-x=15,则12=15 (舍)
当x≥9时,原方程可化为:x+3+x-9=15,解得x=10.5
综上:点P对应的数x=-4.5或10.5时,它到点A、点B的距离之和为15;
(3)分两种情况:①点P在点Q左侧时,
设y分钟后P、Q两点之间的距离为8.
根据题意,得 9-3y+3+y=8,
2y=4,
解得y=2;
P点表示的数是-3-1×2=-5、Q点表示的数是9-3×2=3.
②点P在点Q右侧时,
设z分钟后P、Q两点之间的距离为8.
根据题意,得-3-z-9+3z=8,
2z=20,
解得z=10;
P点表示的数是-3-1×10=-13,Q点表示的数是9-3×10=-21.
故答案为:3;-4.5或10.5.
(2)设点P表示的数为x,则|x+3|+|x-9|=15
当x≤-3时,原方程可化为:-x-3+9-x=15,解得x=-4.5;
当-3<x<9时,原方程可化为:x+3+9-x=15,则12=15 (舍)
当x≥9时,原方程可化为:x+3+x-9=15,解得x=10.5
综上:点P对应的数x=-4.5或10.5时,它到点A、点B的距离之和为15;
(3)分两种情况:①点P在点Q左侧时,
设y分钟后P、Q两点之间的距离为8.
根据题意,得 9-3y+3+y=8,
2y=4,
解得y=2;
P点表示的数是-3-1×2=-5、Q点表示的数是9-3×2=3.
②点P在点Q右侧时,
设z分钟后P、Q两点之间的距离为8.
根据题意,得-3-z-9+3z=8,
2z=20,
解得z=10;
P点表示的数是-3-1×10=-13,Q点表示的数是9-3×10=-21.
故答案为:3;-4.5或10.5.
点评:此题主要考查了一元一次方程的应用以及数轴上点的坐标与距离表示方法等知识,利用分类讨论得出是解题关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 已知:如图,AB∥CD,求证:∠BED=∠B-∠D.
已知:如图,AB∥CD,求证:∠BED=∠B-∠D.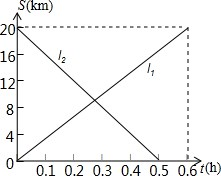 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系. 如图,已知△OAB∽△OCD,且DC∥AB,请写出这对相似三角形对应角和对应边的比例式.
如图,已知△OAB∽△OCD,且DC∥AB,请写出这对相似三角形对应角和对应边的比例式. 如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?
如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?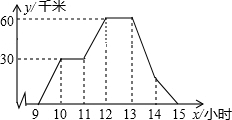 A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)
A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)