题目内容
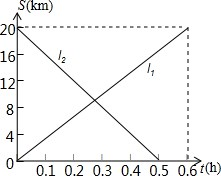甲、乙两辆摩托车分别从A、B两地出发相向而行，图中l1、l2分别表示两辆摩托车与A地的距离s（千米）与行驶时间t（小时）之间的函数关系．（1）哪俩摩托车的速度较快？
（2）经过多长时间，甲车行驶到A、B两地的中点；
（3）经过多长时间，两车相距5km．
考点：一次函数的应用
专题：计算题,行程问题
分析：（1）通过函数图象可以得出甲走到B地的时间是0.6小时，乙走到A地的时间是0.5小时，就可以得出用的时间少就可以得出结论；
（2）根据图形可以先求出甲的速度，再根据时间=路程÷速度就可以得出结论；
（3）根据图象先求出甲乙的速度，再由时间=路程÷速度就可以得出结论．
（2）根据图形可以先求出甲的速度，再根据时间=路程÷速度就可以得出结论；
（3）根据图象先求出甲乙的速度，再由时间=路程÷速度就可以得出结论．
解答：解：（1）由函数图象得
甲走到B地的时间是0.6小时，乙走到A地的时间是0.5小时，
∵0.6＞0.5，
∴乙的速度较快；
（2）由函数图象，得
甲的速度为：20÷0.6=
，
∴甲车行驶到A、B两地的中点的时间为：10÷
=0.3小时．
答：经过0.3小时，甲车行驶到A、B两地的中点；
（3）由函数图象，得
乙的速度为：20÷0.5=40km/h，
∴（20-5）÷（40+
）=
小时，
（20+5）÷（40+
）=
小时．
答：经过
小时或
小时，两车相距5km．
甲走到B地的时间是0.6小时，乙走到A地的时间是0.5小时，
∵0.6＞0.5，
∴乙的速度较快；
（2）由函数图象，得
甲的速度为：20÷0.6=
| 100 |
| 3 |
∴甲车行驶到A、B两地的中点的时间为：10÷
| 100 |
| 3 |
答：经过0.3小时，甲车行驶到A、B两地的中点；
（3）由函数图象，得
乙的速度为：20÷0.5=40km/h，
∴（20-5）÷（40+
| 100 |
| 3 |
| 9 |
| 44 |
（20+5）÷（40+
| 100 |
| 3 |
| 15 |
| 44 |
答：经过
| 9 |
| 44 |
| 15 |
| 44 |
点评：本题考查了一次函数的图象的性质的运用，行程问题的数量关系的运用，速度=路程÷时间的运用，解答时运用行程问题的数量关系速度=路程÷时间是关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，OA=OB，OC=OD，∠AOC=∠BOD=90°，M、N分别是AC、BD的中点，连接MN、ON，求证：MN=
已知如图：数轴上两点A、B对应的数分别为-3，9，点P为数轴上一动点，其对应的数为x．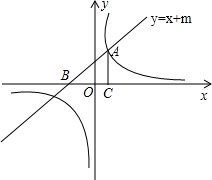
如图，已知直线y=x+m与双曲线y=
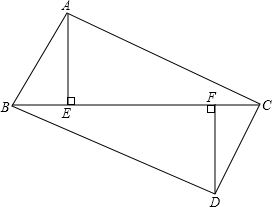如图所示，点B、E、F、C在同一条直线上，有AE⊥BC．DF⊥BC，垂足分别为点E、F，且AC=DB，BE=CF，求证：