题目内容
已知a2+b2+c2-ab-3b-2c+4=0,则a+b+c的值为 .
考点:因式分解的应用
专题:因式分解
分析:首先分组利用完全平方公式分解因式,利用非负数的性质求得a、b、c的数值,进一步求得a+b+c的值即可.
解答:解:a2+b2+c2-ab-3b-2c+4=0
a2-ab+
b2+
(b2-4b+4)+c2-2c+1=0
(a-
b)2+
(b-2)2+(c-1)2=0
∴a-
b=0,
(b-2)=0,c-1=0
∴a=1,b=2,c=1,
则a+b+c=4.
故答案为:4.
a2-ab+
| 1 |
| 4 |
| 3 |
| 4 |
(a-
| 1 |
| 2 |
| 3 |
| 4 |
∴a-
| 1 |
| 2 |
| 3 |
| 4 |
∴a=1,b=2,c=1,
则a+b+c=4.
故答案为:4.
点评:此题考查利用完全平方公式因式分解,注意分组的技巧和方法.

练习册系列答案
相关题目
 已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.
已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x. 如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有
如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有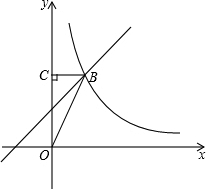 如图,一次函数y=x+b与反比例函数y=
如图,一次函数y=x+b与反比例函数y=