题目内容
 如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?
如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?考点:切线的性质,垂径定理
专题:几何图形问题,证明题
分析:AB=CD,理由为:连接OM,ON,OA,OC,利用切线的性质得到OM与AB垂直,ON与CD垂直,利用垂径定理得到M、N分别为AB、CD的中点,再利用HL得到三角形AOM与三角形CON全等,进而得到AM=CN,即可得证.
解答: 解:AB=CD,理由为:
解:AB=CD,理由为:
连接OM,ON,OA,OC,
∵AB、CD与小圆O相切,
∴OM⊥AB,ON⊥CD,
∴M、N分别为AB、CD的中点,
∴AM=BM=
AB,CN=DN=
CD,
在Rt△AOM和Rt△CON中,
,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
则AB=CD.
答:AB、CD是相等.
 解:AB=CD,理由为:
解:AB=CD,理由为:连接OM,ON,OA,OC,
∵AB、CD与小圆O相切,
∴OM⊥AB,ON⊥CD,
∴M、N分别为AB、CD的中点,
∴AM=BM=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOM和Rt△CON中,
|
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
则AB=CD.
答:AB、CD是相等.
点评:此题考查了切线的性质,以及垂径定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 如图,菱形ABCD中,∠ABC=60°,E是BC延长线上的一点,F是对角线AC上的一点,AF=CE,连接BF、EF.
如图,菱形ABCD中,∠ABC=60°,E是BC延长线上的一点,F是对角线AC上的一点,AF=CE,连接BF、EF. 已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.
已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.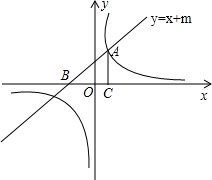 如图,已知直线y=x+m与双曲线y=
如图,已知直线y=x+m与双曲线y=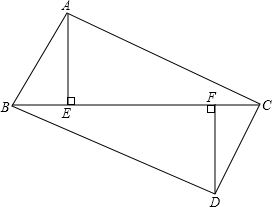 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证: 如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有
如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有