题目内容
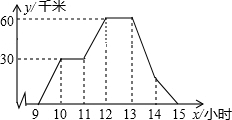 A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)
A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)(1)从折线图可以看出,骑车人一共休息
(2)请在图中画出9点至15点之间客车与A地距离y随x变化的函数图象.
(3)通过计算说明,何时骑车人与客车第二次相遇?
考点:一次函数的应用
专题:计算题,图表型,待定系数法
分析:(1)观察图象可以看出距离没有发生变化而时间在变化说明骑车人在休息,则由图形可以得出答案.
(2)由于客车9点从B地出发,以60千米/小时时的速度匀速行驶,由此可以确定它到A、B两站的时刻,根据时刻和速度即可画出图象;
(3)根据题意,客车一小时行驶60千米,故它的图象是两小时一个来回.从左向右看,两条折线的第二个交点就是它们第二次相遇.求出EF的函数解析式就可以了,找到特殊点(10,0)和(11,60)利用待定系数法可以求出其解析式.
(2)由于客车9点从B地出发,以60千米/小时时的速度匀速行驶,由此可以确定它到A、B两站的时刻,根据时刻和速度即可画出图象;
(3)根据题意,客车一小时行驶60千米,故它的图象是两小时一个来回.从左向右看,两条折线的第二个交点就是它们第二次相遇.求出EF的函数解析式就可以了,找到特殊点(10,0)和(11,60)利用待定系数法可以求出其解析式.
解答:解:(1)依题意得:骑车人一共休息两次;
故答案为:两.
(2)如图:

(3)设直线EF所表示的函数解析式为y=kx+b.
把E(10,0),F(11,60)分别代入y=kx+b,得
,
解得
.
故直线EF所表示的函数解析式为y=50x-500.
把y=30代入y=60x-500得30=60x-600
解得x=10.5,即10时30分.
答:10时30分骑车人与客车第二次相遇.
故答案为:两.
(2)如图:

(3)设直线EF所表示的函数解析式为y=kx+b.
把E(10,0),F(11,60)分别代入y=kx+b,得
|
解得
|
故直线EF所表示的函数解析式为y=50x-500.
把y=30代入y=60x-500得30=60x-600
解得x=10.5,即10时30分.
答:10时30分骑车人与客车第二次相遇.
点评:本题考查的是函数的图象,此题比较复杂,首先是正确理解题意,这要求仔细观察图象,从图象中得到需要的信息,关键知道它们走的方向不同.此外还用到了待定系数法求函数解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少? 已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.
已知如图:数轴上两点A、B对应的数分别为-3,9,点P为数轴上一动点,其对应的数为x.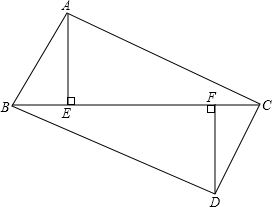 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证: 如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有
如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有