题目内容
15.半径为4的圆内接正三角形、正方形的边长之积是16$\sqrt{6}$.分析 根据正多边形的中心角的求法公式分别求出中心角,根据正弦的定义求出边长,计算即可.
解答 解:正三角形的中心角是$\frac{360°}{3}$=120°,
则边长是:2×4sin60°=4$\sqrt{3}$,
正方形的中心角=$\frac{360°}{4}$=90°,
∴正方形的边长是:$\sqrt{{4}^{2}{+4}^{2}}$=4$\sqrt{2}$,
∴正三角形、正方形的边长之积是4$\sqrt{3}$×4$\sqrt{2}$=16$\sqrt{6}$,
故答案为:16$\sqrt{6}$.
点评 本题考查的是正多边形和圆,掌握正多边形的中心角的求法、掌握锐角三角函数的定义、熟记特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
18.下列命题中,真命题有( )
①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形对的一个外角大于任何一个内角;④如果a2=b2,那么a=b.
①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形对的一个外角大于任何一个内角;④如果a2=b2,那么a=b.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.且a+b-c=m,①填表:②观察下表猜想:m×l=4S.(用含s的代数式表示)③证明②中的结论.
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
 如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E
如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E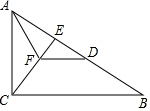 如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.
如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.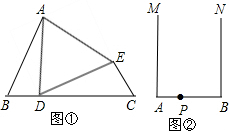
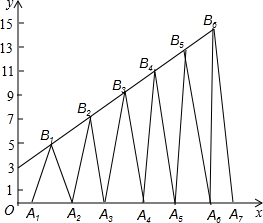 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.