Question

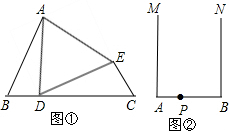
10．学之道在于悟．希望同学们在问题（1）解决过程中有所悟，再继续探索研究问题（2）．
（1）如图①，∠B=∠C，BD=CE，AB=DC．
①求证：△ADE为等腰三角形．
②若∠B=60°，求证：△ADE为等边三角形．
（2）如图②，射线AM与BN，MA⊥AB，NB⊥AB，点P是AB上一点，在射线AM与BN上分别作点C、点D满足：△CPD为等腰直角三角形．（要求：利用直尺与圆规，不写作法，保留作图痕迹）

Answer 1

分析 （1）①先根据∠B=∠C，BD=CE，AB=DC，判定△ABD≌DCE，得出AB=DC，进而得到△ADE为等腰三角形；
②根据△ABD≌△DCE，得出∠BAD=∠CDE，再根据∠ADC=∠B+∠BAD，∠ADC=∠ADE+∠EDC，得到∠ADE=∠B=60°，最后判定等腰△ADE为等边三角形；
（2）分三种情况讨论：∠CPD为直角顶点；∠PCD是直角顶点；∠PDC是直角顶点，分别进行画图即可．第一种情况：使得AP=BD，BP=AC；第二种情况：使得AC=AB，CE=AP，BD=AE；第三种情况：使得BD=AB，DF=BP，AC=BF．

解答 （1）①证明：在△ABD和△DCE中，
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$，
∴△ABD≌△DCE（SAS），
∴DA=DE，即△ADE为等腰三角形；

②解：∵△ABD≌△DCE，
∴∠BAD=∠CAE，
∵∠B=60°，
∴∠BAD+∠ADB=120°，
∴∠CAE+∠ADB=120°，
∴∠ADE=60°，又△ADE为等腰三角形，
∴△ADE为等边三角形；
（2）有三种情况，PC=PD、CP=CD、DC=DP，
如图所示：

点评 本题主要考查了等腰直角三角形的性质，等边三角形的判定与性质以及全等三角形的判定与性质的综合应用，解决问题的关键是掌握全等三角形的判定方法．解题时注意分类讨论思想的运用．