题目内容
4.先阅读下列解题过程,然后解答问题(1)、(2)解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=-1;
当x+3<0时,原方程可化为:x+3=-2,解得x=-5.
所以原方程的解是x=-1,x=-5.
(1)解方程:|3x-1|-5=0;
(2)探究:当b为何值时,方程|x-2|=b+1 ①无解;②只有一个解;③有两个解.
分析 (1)先移项得到)|3x-1|=5,利用绝对值的意义得到3x-1=5或3x-1=-5,然后分别解两个一次方程;
(2)利用绝对值的意义讨论:当b+1<0或b+1=0或b+1>0时确定方程的解的个数,
解答 解:(1)|3x-1|=5,
3x-1=5或3x-1=-5,
所以x=2或x=-$\frac{4}{3}$;
(2)∵|x-2|≥0,
∴当b+1<0,即b<-1时,方程无解;
当b+1=0,即b=-1时,方程只有一个解;
当b+1>0,即b>-1时,方程有两个解.
点评 本题考查了含绝对值符号的一元一次方程:解含绝对值符号的一元一次方程要根据绝对值的性质和绝对值符号内代数式的值分情况讨论,即去掉绝对值符号得到一般形式的一元一次方程,再求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
14.手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:
则这两个模型都制作完成所需的最短时间为( )
| 工序 时间 模型 | 打磨(A组) | 组装(B组) |
| 模型甲 | 9分钟 | 5分钟 |
| 模型乙 | 6分钟 | 11分钟 |
| A. | 20分钟 | B. | 22分钟 | C. | 26分钟 | D. | 31分钟 |
13.已知关于x的一元二次方程ax2-2x+1=0有两个不相等的实数根,则实数a的取值范围是( )
| A. | a<-1 | B. | a≠0 | C. | a<1且a≠0 | D. | a<-1或a≠0 |

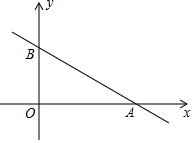 如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.
如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.