题目内容
20.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.且a+b-c=m,①填表:②观察下表猜想:m×l=4S.(用含s的代数式表示)③证明②中的结论.| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
分析 ①根据周长的定义,直角三角形的面积公式求解即可;
②根据求得的a+b-c与l的值,总结其规律,写出即可;
③用m、c的式子表示出a、b,分别表示出其周长及面积,用面积除以周长即可完成证明.
解答 解:①l=3+4+5=12,
l×m=12×2=24,
S=3×4÷2=6;
l=5+12+15=30,
l×m=30×4=120,
S=5×12÷2=30;
l=8+15+17=40,
l×m=40×6=240,
S=8×15÷2=60;
填表如下:
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
③证明:∵a+b-c=m,
∴a+b=m+c,
∴a2+2ab+b2=m2+2mc+c2,
又∵a2+b2=c2,
∴2ab=m2+2mc,
∴S=$\frac{1}{2}$ab=$\frac{1}{4}$m(m+2c),
∴4S=m(a+b-c+2c)=m(a+b+c)=m×l.
故答案为:4S;24,6;120,30;240,60.
点评 本题考查了勾股定理的相关知识,在完成证明时候关键是用到了完全平方公式,是一道中档考题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知等腰三角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
 -3x+2=x2-5x+1.
-3x+2=x2-5x+1.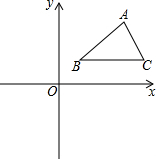 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).
