题目内容
5.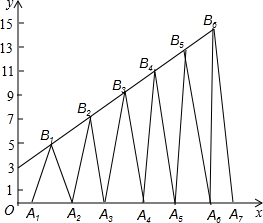 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
分析 根据一次函数图象上点的坐标特征,求得点B1、B2、B3的纵坐标,然后由三角形的面积公式求得S1,S2…Sn;由此得出规律,即可求得S2017-S2016的值.
解答  解:∵B1(1,y1)、B2(2,y2)、B3(3,y3),…,在直线y=2x+3上,
解:∵B1(1,y1)、B2(2,y2)、B3(3,y3),…,在直线y=2x+3上,
∴y1=2×1+3=5,y2=2×2+3=7,y3=2×3+3=9,y4=2×4+3=11,…,yn=2n+3;
又∵OA1=a(0<a<1),
∴S1=$\frac{1}{2}$×2×(1-a)×5=5(1-a);
S2=$\frac{1}{2}$×2×[2-a-2×(1-a)]×7=7a;
S3=$\frac{1}{2}$×2×{3-a-2×(1-a)-2×[2-a-2×(1-a)]}×9=9(1-a);
S4=$\frac{1}{2}$×2×[1-(1-a)]×11=11a;
…
∴Sn=(2n+3)(1-a)(n是奇数);Sn=(2n+3)a(n是偶数),
∴S2017-S2016=(2×2017+3)(1-a)-(2×2016+3)a=4037-8072a.
故答案是:4037-8072a.
点评 本题考查了一次函数图象上点的坐标特征,等腰三角形的性质的综合应用.解答此题的关键是根据已知条件找出规律:Sn=(2n+3)(1-a)(n是奇数);Sn=(2n+3)a(n是偶数).

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.已知关于x的一元二次方程ax2-2x+1=0有两个不相等的实数根,则实数a的取值范围是( )
| A. | a<-1 | B. | a≠0 | C. | a<1且a≠0 | D. | a<-1或a≠0 |
20.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
| A. | a:b:c=3:5:6 | B. | a2-c2=b2 | C. | ∠A-∠B=∠C | D. | a=$\sqrt{7}$,b=3,c=4 |
17.若点P(a,b)在第四象限内,则Q(b,-a)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15. 如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
 如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )| A. | 56° | B. | 66° | C. | 24° | D. | 34° |
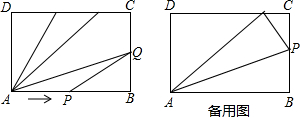

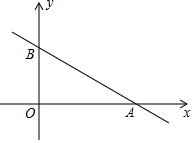 如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.
如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.