题目内容
3.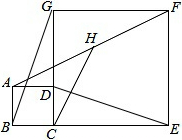 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:(1)BG=DE;
(2)CH=$\frac{1}{2}$AF.
分析 (1)由正方形的性质得出∠BCD=∠DCE=90°,BC=DC,CG=CE,由SAS证明△BCG≌△DCE,得出对应边相等即可;
(2)连接AC、CF,由正方形的性质得出∠ACD=∠FCG=45°,证出△ACF是直角三角形,由直角三角形斜边上的中线性质即可得出结论.
解答 证明:(1)∵四边形ABCD和CEFG均为正方形,
∴∠BCD=∠DCE=90°,BC=DC,CG=CE,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCD=∠DCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,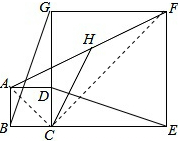
∴△BCG≌△DCE(SAS),
∴BG=DE;
(2)连接AC、CF,如图所示:
∵四边形ABCD和CEFG均为正方形,
∴∠ACD=∠FCG=45°,
∴∠ACF=45°+45°=90°,
即△ACF是直角三角形,
∵H是AF的中点,
∴CH=$\frac{1}{2}$AF.
点评 本题考查了正方形的性质,全等三角形的判定由V型在,直角三角形斜边上的中线性质;熟练掌握正方形的性质,证明三角形全等是解决问题(1)的关键.

练习册系列答案
相关题目
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. | 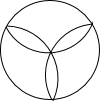 | D. | 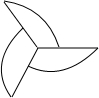 |
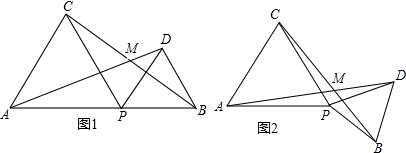
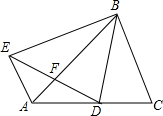 在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.
在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.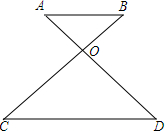 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3.