题目内容
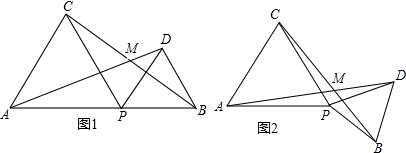
13.如图1,点P是线段AB上的动点(P不与A、B重合),分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD,AD和BC交于点M.(1)求证:AD=BC;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α(α<60°),如图2所示,在旋转过程中,∠AMC的度数是否与α的大小有关?证明你的结论.
分析 (1)只要证明△BPC≌△DPA即可.
(2)先证明△BPC≌△DPA得到∠BCP=∠DAP,求出∠AMC的大小即可解决问题.
解答 解:(1)如图1,∵△APC和△BPD是等边三角形,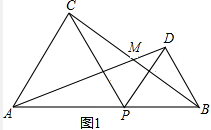 ∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∵∠BPC=180°-60°,∠DPA=180°-60°,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
$\left\{\begin{array}{l}{CP=AP}\\{∠BPC=∠DPA}\\{DP=PB}\end{array}\right.$,
∴△BPC≌△DPA,
∴AD=BC.
(2)∠AMC的度数与α的大小无关,理由如下:
如图2,∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,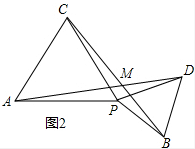 ∴∠BPC=∠DPA,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
$\left\{\begin{array}{l}{BP=DP}\\{∠BPC=∠DPA}\\{PC=PA}\end{array}\right.$,
∴△BPC≌△DPA,
∴∠BCP=∠DAP,
∴∠AMC=180°-∠MCP-∠PCA-∠MAC
=120°-∠BCP-∠MAC
=120°-(∠DAP+∠MAC)
=120°-∠PAC
=60°,
∴∠AMC的度数与α无关.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,所以中考常考题型.

练习册系列答案
相关题目
5.下列有理式中是分式的是( )
| A. | $\frac{1}{5}(x+y)$ | B. | $\frac{a}{3}$ | C. | $\frac{ab}{2}+\frac{1}{c}$ | D. | $\frac{x}{2}+y$ |
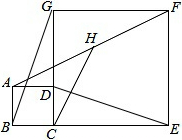 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证: 如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.
如图,在矩形ABCD中,BC=2AB.以点B为圆心,BC长为半径作弧交AD于点E,连结BE.若AB=1,则DE的长为2-$\sqrt{3}$.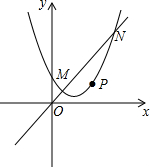 如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.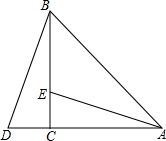 如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证: