题目内容
18.计算:(1)3($\sqrt{2}$+$\sqrt{3}$)+3($\sqrt{2}$-2$\sqrt{3}$);
(2)|2-$\sqrt{2}$|+|$\sqrt{3}$-3|+|3-π|+$\sqrt{(π-4)^{2}}$;
(3)$\sqrt{3}$($\sqrt{3}$-$\frac{2}{\sqrt{3}}$).
分析 (1)根据二次根式的混合计算解答即可;
(2)根据二次根式和绝对值的化简解答即可;
(3)根据二次根式的混合计算解答即可.
解答 解:(1)3($\sqrt{2}$+$\sqrt{3}$)+3($\sqrt{2}$-2$\sqrt{3}$)=$3\sqrt{2}+3\sqrt{3}+3\sqrt{2}-6\sqrt{3}=6\sqrt{2}-3\sqrt{3}$;
(2)|2-$\sqrt{2}$|+|$\sqrt{3}$-3|+|3-π|+$\sqrt{(π-4)^{2}}$=$2-\sqrt{2}+3-\sqrt{3}+π-3+4-π=6-\sqrt{2}-\sqrt{3}$;
(3)$\sqrt{3}$($\sqrt{3}$-$\frac{2}{\sqrt{3}}$)=3-2=1.
点评 此题考查二次根式的混合计算,关键是根据二次根式的混合计算顺序解答.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
9.设a=$\sqrt{2}-1$,b=$\sqrt{5}$-2,c=$\sqrt{10}$-3.则a、b、c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
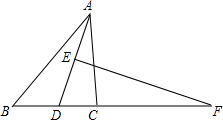 如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.
如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.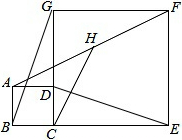 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证: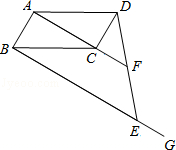 如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.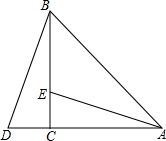 如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证: