题目内容
11.已知在△ABC中,D是AB上一点,E是AC上一点,且DE∥BC,F为BC上一点,AF与DE相交于点G.若AD:BD=2:1,BC=2.4cm,求:(1)DE的长;
(2)$\frac{AG}{AF}$的值;
(3)S△ABC:S△ADE.
分析 (1)由平行线得出△ADE∽△ABC,得出比例式$\frac{AD}{AB}$=$\frac{DE}{BC}$,即可得出结果;
(2)由平行线得出△BAF∽△DAG,得出比例式,即可得出结果;
(3)由比例的性质得出$\frac{AB}{AD}$=$\frac{3}{2}$,由平行线得出△ABC∽△ADE,由相似三角形的性质即可得出结果.
解答 解:如图所示: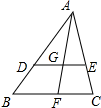
(1)∵AD:DB=2:1,
∴AD:AB=2:3,
∵DE‖BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{2}{3}$=$\frac{DE}{2.4}$,
解得:DE=1.6(cm);
(2)∵DE‖BC,
∴△BAF∽△DAG,
∴$\frac{AG}{AF}$=$\frac{AD}{AB}$=$\frac{2}{3}$;
(3)∵AD:AB=2:3,
∴$\frac{AB}{AD}$=$\frac{3}{2}$,
∵DE‖BC,
∴△ABC∽△ADE,
∴$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=($\frac{AB}{AD}$)2=$\frac{9}{4}$.
点评 本题考查了相似三角形的判定与性质、比例的性质;熟练掌握相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.如果一个角的补角是110°,则这个角的余角的度数是( )
| A. | 30° | B. | 20° | C. | 70° | D. | 110° |
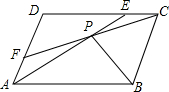 ?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.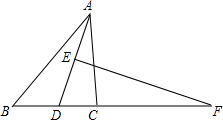 如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.
如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC. 如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.
如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.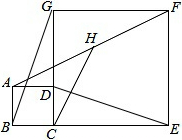 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证: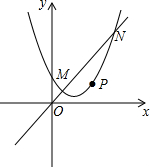 如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.
如图,抛物线y=ax2+bx+c(a≠0)与直线y=kx(k≠0)相交于点M(1,1),N(3,3),且这条抛物线的对称轴为x=1.