题目内容
8.矩形ABCD中,AB=3,BC=4,如果分别以A、C为圆心的两圆外切,点D在圆C内,点B在圆C外,那么圆A的半径r的取值范围是8<r<9或1<r<2.分析 首先根据点D在⊙C内,点B在⊙C外,求得⊙C的半径是大于3而小于4;再根据勾股定理求得AC=5,最后根据两圆的位置关系得到其数量关系.
解答 解:∵在矩形ABCD中,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵点D在⊙C内,点B在⊙C外,
∴⊙C的半径R的取值范围为:3<R<4,
∴当⊙A和⊙C内切时,圆心距等于两圆半径之差,则r的取值范围是8<r<9;
当⊙A和⊙C外切时,圆心距等于两圆半径之和是5,设⊙C的半径是Rc,即Rc+r=5,
又∵3<Rc<4,
则r的取值范围是1<r<2.
所以半径r的取值范围是8<r<9或1<r<2.
故答案为:8<r<9或1<r<2.
点评 此题综合考查了点和圆的位置关系以及两圆的位置关系与数量关系之间的等价关系.同时注意勾股定理的运用.特别注意两圆相切,可能内切或外切.

练习册系列答案
相关题目
20.如果一个角的补角是110°,则这个角的余角的度数是( )
| A. | 30° | B. | 20° | C. | 70° | D. | 110° |
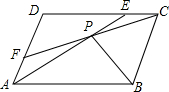 ?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC. 如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.
如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.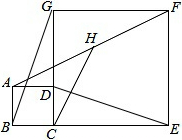 如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证:
如图,D点在边CG上,四边形ABCD和CEFG均为正方形,H是AF的中点.求证: 已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.