题目内容
13. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.
分析 (1)根据题意画出图形,再利用相似三角形的判定与性质得出EO:OF=3:1,进而得出EO的长即可得出答案;
(2)由题意可知,AE,AC不可能与x轴垂直,再得出△EFA∽△AFC,求出m的值,进而得出答案.
解答 解:(1)如图所示:设此抛物线对称轴与x轴交于点F,
∴S△DEC:S△AEC=DO:AF=3:4,
∵DO∥AF,
∴△EDO∽△EAF,
∴EO:EF=DO:AF=3:4,
∴EO:OF=3:1,
由y=mx2-2mx+n(m<0)得:A(1,n-m),D(0,n),
∴OF=1,
∴EO=3,
∴E(-3,0);
(2)∵DO:AF=3:4,
∴$\frac{n}{n-m}$=$\frac{3}{4}$,
∴n=-3m,
∴y=mx2-2mx-3m=m(x2-2x-3)
=m(x-3)(x+1),
∴B(-1,0),C(3,0),A(1,-4m),
由题意可知,AE,AC不可能与x轴垂直,
∴若△AEC为直角三角形,则∠EAC=90°,
又∵AF⊥EC,可得△EFA∽△AFC,
∴$\frac{EF}{AF}$=$\frac{AF}{CF}$,即$\frac{4}{-4m}$=$\frac{-4m}{2}$,
∵m<0,
∴m=-$\frac{\sqrt{2}}{2}$,
∴二次函数解析式为:y=-$\frac{\sqrt{2}}{2}$x2+$\sqrt{2}$x+$\frac{3\sqrt{2}}{2}$.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,正确表示出n,m的关系是解题关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
3.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”,应先假设这个直角三角形中( )
| A. | 有一个锐角小于45° | B. | 每一个锐角都小于45° | ||
| C. | 有一个锐角大于45° | D. | 每一个锐角都大于45° |
4.计算sin60°+cos45°的值等于( )
| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
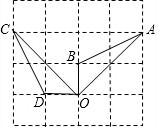 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针旋转到△COD的位置,则旋转角为90°.
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针旋转到△COD的位置,则旋转角为90°.
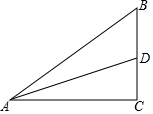 如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.
如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.