题目内容
3．用反证法证明“在直角三角形中，至少有一个锐角不大于45°”，应先假设这个直角三角形中（ ）| A． | 有一个锐角小于45° | B． | 每一个锐角都小于45° | ||
| C． | 有一个锐角大于45° | D． | 每一个锐角都大于45° |
分析 用反证法证明命题的真假，应先按符合题设的条件，假设题设成立，再判断得出的结论是否成立即可．
解答 解：用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，
应先假设每一个锐角都大于45°．
故选：D．
点评 本题考查了反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
18．
如图，正方形ABCD的边长为2，连接BD，先以D为圆心，DA为半径作弧AC，再以D为圆心，DB为半径作弧BE，且D、C、E三点共线，则图中两个阴影部分的面积之和是（ ）
如图，正方形ABCD的边长为2，连接BD，先以D为圆心，DA为半径作弧AC，再以D为圆心，DB为半径作弧BE，且D、C、E三点共线，则图中两个阴影部分的面积之和是（ ）| A． | $\frac{1}{2}$π | B． | $\frac{1}{2}π$+1 | C． | π | D． | π+1 |
12．
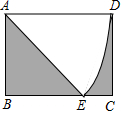在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）
在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）| A． | $\frac{π}{4}$ | B． | 2$\sqrt{2}$-$\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | 2$\sqrt{2}$-$\frac{π}{2}$ |
在平面直角坐标系xOy中，抛物线y=mx2-2mx+n（m＜0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴正半轴交于点D，连接AD并延长交x轴于E，连AC、DC．S△DEC：S△AEC=3：4．