题目内容
1．当$\frac{a-b}{a+b}$=4时，求代数式$\frac{2a-2b}{a+b}$-$\frac{4a+4b}{3a-3b}$的值．分析 原式整理后，将已知等式及倒数的值代入计算即可求出值．
解答 解：∵$\frac{a-b}{a+b}$=4，
∴原式=2×$\frac{a-b}{a+b}$-$\frac{4}{3}$×$\frac{a+b}{a-b}$=8-$\frac{1}{3}$=7$\frac{2}{3}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
6．一列数a1，a2，a3，…满足条件：a1=$\frac{1}{2}$，an=$\frac{1}{1{-a}_{n-1}}$（n≥2，且n为整数），则a2017等于（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
在平面直角坐标系xOy中，抛物线y=mx2-2mx+n（m＜0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴正半轴交于点D，连接AD并延长交x轴于E，连AC、DC．S△DEC：S△AEC=3：4．
6．若不等式a（x-1）-5（2x-3）≥4-3x的解集为x≤2，则a的值为（ ）
| A． | 1 | B． | 2 | C． | -2 | D． | 3 |
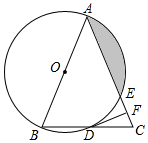如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为F．