题目内容
4．计算sin60°+cos45°的值等于（ ）| A． | $\frac{1+\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | C． | $\frac{1+\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
分析 根据特殊角三角函数值，可得答案．
解答 解：sin60°+cos45°=$\frac{\sqrt{3}+\sqrt{2}}{2}$，
故选：B．
点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12．
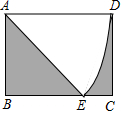在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）
在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）| A． | $\frac{π}{4}$ | B． | 2$\sqrt{2}$-$\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | 2$\sqrt{2}$-$\frac{π}{2}$ |
19．
如图，在⊙O中，AC∥OB，∠BAC=25°，则∠ADB的度数为（ ）
如图，在⊙O中，AC∥OB，∠BAC=25°，则∠ADB的度数为（ ）| A． | 55° | B． | 60° | C． | 65° | D． | 70° |
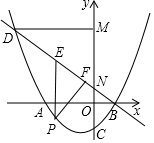如图，抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点，其中点B（2，0），交y轴于点C（0，-$\frac{5}{2}$）．直线y=mx+$\frac{3}{2}$过点B与y轴交于点N，与抛物线的另一个交点是D，点P是直线BD下方的抛物线上一动点（不与点B、D重合），过点P作y轴的平行线，交直线BD于点E，过点D作DM⊥y轴于点M．
在平面直角坐标系xOy中，抛物线y=mx2-2mx+n（m＜0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴正半轴交于点D，连接AD并延长交x轴于E，连AC、DC．S△DEC：S△AEC=3：4．