题目内容
6.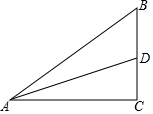 如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.
如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.(1)比较∠BAD和∠DAC的大小.
(2)求sin∠BAD.
分析 (1)要比较∠BAD和∠DAC的大小,只要比较它们的正弦值的大小即可,根据题目中的数据可以求得它们的正弦值,从而可以解答本题;
(2)根据题目中的数据可以求得DE和AD的长,从而可以求得sin∠BAD.
解答 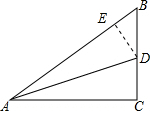 解:(1)过点D做AB的垂线,垂足记为E,
解:(1)过点D做AB的垂线,垂足记为E,
则sin∠DAE=$\frac{DE}{AD}$,sin∠DAC=$\frac{CD}{AD}$,
∵BC=2,AD为中线,
∴BD=CD=1,
∵BD>DE,
∴CD>DE,
∴sin∠DAE<sin∠DAC,
∴∠BAD<∠DAC;
(2)∵在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线,
∴BD=CD=1,AB=$\sqrt{13}$,
∴$\frac{BD•AC}{2}=\frac{AB•DE}{2}$,AD=$\sqrt{A{C}^{2}+C{D}^{2}}=\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$,
解得,DE=$\frac{3\sqrt{13}}{13}$,
∴sin∠BAD=$\frac{DE}{AD}=\frac{\frac{3\sqrt{13}}{13}}{\sqrt{10}}$=$\frac{3\sqrt{130}}{130}$.
点评 本题考查解直角三角形,解答本题的关键是明确题意,利用锐角三角函数和勾股定理解答.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.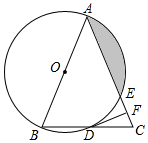 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.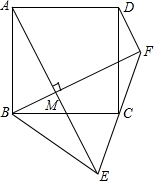 正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.
正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.