题目内容
8.已知关于x的一元二次方程(3a-1)x2-ax+$\frac{1}{4}$=0有两个相等的实数根,求代数式a+1+$\frac{1}{a}$的值.分析 先根据一元二次方程的定义以及根的判别式得到3a-1≠0且△=a2-4×(3a-1)×$\frac{1}{4}$=0,则a2-3a+1=0,再将代数式a+1+$\frac{1}{a}$通分后把a2+1=3a代入计算即可.
解答 解:根据题意得3a-1≠0且△=a2-4×(3a-1)×$\frac{1}{4}$=0,即a2-3a+1=0,
所以原式=$\frac{{a}^{2}+a+1}{a}$=$\frac{3a+a}{a}$=4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
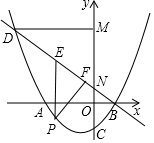 如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.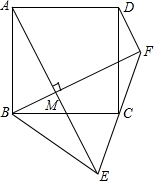 正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.
正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.