题目内容
12.若|a|=3,|b|=5,且a>b,则a-b=8或2.分析 先由绝对值的性质求得a、b的值,然后根据全a>b,确定出a、b的取值情况,最后代入计算即可.
解答 解:∵|a|=3,|b|=5,
∴a=±3,b=±5.
∵a>b,
∴a=3,b=-5或a=-3,b=-5.
当a=3,b=-5时,a-b=3-(-5)=3+5=8;
当a=-3,b=-5时a-b=-3-(-5)=-3+5=2.
故答案为:8或2.
点评 本题主要考查的是绝对值、有理数的减法,由a>b得到a=3,b=-5或a=-3,b=-5是解题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
7. “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
 “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
| 落在“铅笔”区域的频率$\frac{m}{n}$ | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度.
 在△ABC中,∠A=50°,OB,OC分别平分∠ABC和∠ACB,则∠BOC=115度.
在△ABC中,∠A=50°,OB,OC分别平分∠ABC和∠ACB,则∠BOC=115度. 在Rt△ABC中,∠C=90°,∠B=2∠A,求∠B,∠A的度数.
在Rt△ABC中,∠C=90°,∠B=2∠A,求∠B,∠A的度数.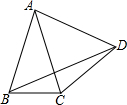 如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.