题目内容
17. 在△ABC中,∠A=50°,OB,OC分别平分∠ABC和∠ACB,则∠BOC=115度.
在△ABC中,∠A=50°,OB,OC分别平分∠ABC和∠ACB,则∠BOC=115度.
分析 由三角形内角和定理求出∠ABC+∠ACB=180°-∠A=130°,由角平分线的定义得出∠OBC+∠OCB=65°,再由三角形内角和定理即可求出∠BOC的度数.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故答案为:115.
点评 本题考查的是三角形内角和定理、角平分线的定义,熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
8.今年弟弟10岁,姐姐12岁,经过t年后,姐弟年龄之和为( )
| A. | (12+t)岁 | B. | (11+t)岁 | C. | (22+2t)岁 | D. | (22+t)岁 |
5.以下列各组数为边长,能组成直角三角形的是( )
| A. | 2,3,4 | B. | 10,8,6 | C. | 8,25,24 | D. | 7,15,12 |
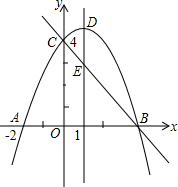 抛物线y=ax2+bx+c(a≠0)与y轴于点C(0,4),与x轴交于点A、B,其中A(-2,0),抛物线对称轴直线x=1与抛物线交于点D,与直线BC交于点E.
抛物线y=ax2+bx+c(a≠0)与y轴于点C(0,4),与x轴交于点A、B,其中A(-2,0),抛物线对称轴直线x=1与抛物线交于点D,与直线BC交于点E. 如图,∠1=100°,∠2=145°,则∠3=65°.
如图,∠1=100°,∠2=145°,则∠3=65°. 小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数关系.根据图象解答下列问题:
小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数关系.根据图象解答下列问题: