题目内容
20.已知AB=AC=BD=k•BE.∠BAC=2∠BED,∠DBE=90°,点O为CE的中点连接AO:(1)如图1,C,D,E在一条直线上,k=1,
①求∠BDE的度数;
②线段AO,CD有怎样的数量关系;
(2)如图2,将△BED绕点B旋转,其他条件不变,求$\frac{CD}{AO}$的值(用含k的式子表示).

分析 (1)①根据等腰直角三角形的性质和已知条件求出∠BDE的度数;
②延长CA至M,使AM=AC,连接BM、EM,证明△EBM≌△DBC,得到CD=EM,根据三角形中位线定理证明AO=$\frac{1}{2}$EM,得到答案;
(2)延长CA至G,使AG=AC,连接BG、EG,证明△GBC∽△EBD和△GBE∽△CBD,根据相似三角形的性质得到答案.
解答 解:(1)①∵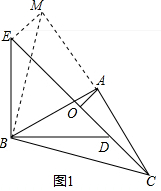 BD=k•BE,k=1,
BD=k•BE,k=1,
∴BD=BE,
又∵∠DBE=90°,
∴∠BDE=45°;
②如图1,延长CA至M,使AM=AC,连接BM、EM,
∵∠BAC=2∠BED,
∴∠BAC=90°,又AB=AC,
∴∠ACB=45°,
∵AM=AC,AB=AC,
∴∠MBC=90°,
∴BM=BC,
∵∠DBE=90°,∠MBC=90°,
∴∠EBM=∠DBC,
在△EBM和△DBC中,
$\left\{\begin{array}{l}{BE=BD}\\{∠EBM=∠DBC}\\{BM=BC}\end{array}\right.$,
∴△EBM≌△DBC,
∴CD=EM,
∵点O为CE的中点,AM=AC,
∴AO=$\frac{1}{2}$EM,
∴AO=$\frac{1}{2}$CD;
(2)CD=2k•OA.
如图2,延长CA至G,使AG=AC,连接BG、EG,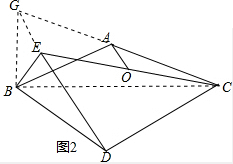
∵AG=AC,AB=AC,
∴∠GBC=90°,
又∵∠DBE=90°,
∴∠EBG=∠DBC,
∵AG=AB,
∴∠ABG=∠AGB,
∴∠BAC=2∠ABG,又∠BAC=2∠BED,
∴∠ABG=∠BED,又∠GBC=∠DBE=90°,
∴△GBC∽△EBD,
∴$\frac{BG}{BC}$=$\frac{BE}{BD}$,又∠ABG=∠AGB,
∴△GBE∽△CBD,
∴$\frac{CD}{GE}$=$\frac{BD}{BE}$=k,
∴CD=k•GE,
∵EO=OC,GA=AC,
∴GE=2OA,
∴CD=2k•OA.
点评 本题考查的是相似三角形、全等三角形的知识的综合运用,掌握全等三角形的判定定理、性质定理和相似三角形的判定定理、性质定理是解题的关键,注意要正确作出辅助线,构造相似三角形.

 黄冈创优卷系列答案
黄冈创优卷系列答案| A. | (12+t)岁 | B. | (11+t)岁 | C. | (22+2t)岁 | D. | (22+t)岁 |
| A. | 2,3,4 | B. | 10,8,6 | C. | 8,25,24 | D. | 7,15,12 |
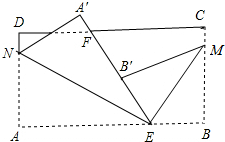 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角. 已知:如图,四边形ABCD中,AB=CD,AD=CB,求证:AB∥CD.
已知:如图,四边形ABCD中,AB=CD,AD=CB,求证:AB∥CD.