题目内容
11.(1)如图1,AC=DC,BC=EC,∠ACD=∠BCE,求证:∠A=∠D.(2)如图2,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,求∠ADP的度数.

分析 (1)由∠ACD=∠BCE可得出∠DCE=∠ACB,结合全等三角形的判定定理SAS即可证出△DCE≌△ACB,由此即可得出结论;
(2)连接OD,由圆内接四边形对角互补可得出∠BAD=60°,由此可知△OAD为等边三角形,再根据切线的性质以及角的计算即可得出结论.
解答 (1)证明:∵∠ACD=∠BCE,
∴∠DCE=∠DCA+∠ACE=∠ACE+∠ECB=∠ACB,
在△DCE和△ACB中,有$\left\{\begin{array}{l}{DC=AC}\\{∠DCE=∠ACB}\\{BC=EC}\end{array}\right.$,
∴△DCE≌△ACB(SAS),
∴∠A=∠D.
(2)解:连接OD,如图所示.
∵在⊙O的内接四边形ABCD中,∠BCD=120°,
∴∠BAD=180°-∠BCD=60°,
∵OA=OD,
∴△OAD为等边三角形,
∴∠ADO=60°.
∵PD为⊙O的切线,D为切点,
∴∠PDO=90°,
∴∠ADP=∠PDO-∠ADO=30°.
点评 本题考查了切线的性质、圆内接四边形的性质以及全等三角形的判定与性质,解题的关键是:(1)证出△DCE≌△ACB;(2)找出△OAD为等边三角形.本题属于中档题,难度不大,解决该题型题目时,找出相等的边角关系证出三角形全等是关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
20. 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )
①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
| A. | ①或④ | B. | ②或③ | C. | ①或③ | D. | ②或④ |
1.下列式子中,正确的是( )
| A. | x3÷x2=x | B. | x3+x2=x5 | C. | x3-x2=x | D. | x3•x2=x6 |
18.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
20.计算${(-\;\frac{1}{2}\;)^0}$的结果是( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 0 | D. | 1 |
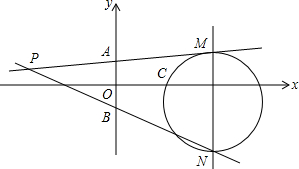 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.