题目内容
9.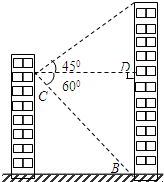 小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为45°,大厦底部B的俯角为60°.求小明家所在居民楼与大厦的距离CD的长度.计算结果保留根号.
小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为45°,大厦底部B的俯角为60°.求小明家所在居民楼与大厦的距离CD的长度.计算结果保留根号.
分析 利用所给角的三角函数用CD表示出AD、BD;根据AB=AD+BD=80米,即可求得居民楼与大厦的距离.
解答 解:设CD=x.
在Rt△ACD中,tan45°=$\frac{AD}{CD}$=1,
∴AD=CD=x,
在Rt△BCD中,tan60°=$\frac{BD}{CD}$=$\sqrt{3}$,
∴BD=$\sqrt{3}$CD=$\sqrt{3}$x,
∵AD+BD=80,
∴x+$\sqrt{3}$x=80,.解得:x=40$\sqrt{3}$-40,
答:小英家所在居民楼与大厦的距离CD是(40$\sqrt{3}$-40)米.
点评 本题考查直角三角形的解法,首先构造直角三角形,再运用三角函数的定义解题,能够造出直角三角形是解题的关键.

练习册系列答案
相关题目
19. 如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
 如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )| A. | 30° | B. | 60° | C. | 120° | D. | 240° |
20.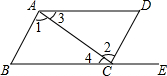 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )
①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
| A. | ①或④ | B. | ②或③ | C. | ①或③ | D. | ②或④ |
4.下列命题中,真命题的个数是( )
①同位角相等;
②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c.
③a,b,c是三条直线,若a∥b,b∥c,则a∥c;
④过一点有且只有一条直线与已知直线平行.
①同位角相等;
②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c.
③a,b,c是三条直线,若a∥b,b∥c,则a∥c;
④过一点有且只有一条直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列式子中,正确的是( )
| A. | x3÷x2=x | B. | x3+x2=x5 | C. | x3-x2=x | D. | x3•x2=x6 |
18.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
20.计算${(-\;\frac{1}{2}\;)^0}$的结果是( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 0 | D. | 1 |
 黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).