题目内容
6.已知正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象交于A,B两点,若点A的坐标为(-2,1),则关于x的方程$\frac{m}{x}$=kx的两个实数根分别为( )| A. | x1=-1,x2=1 | B. | x1=-1,x2=2 | C. | x1=-2,x2=1 | D. | x1=-2,x2=2 |
分析 根据正、反比例函数图象的对称性可得出点A、B关于原点对称,由点A的坐标即可得出点B的坐标,结合A、B点的横坐标即可得出结论.
解答 解:∵正比例函数图象关于原点对称,反比例函数图象关于原点对称,
∴两函数的交点A、B关于原点对称,
∵点A的坐标为(-2,1),
∴点B的坐标为(2,-1).
∴关于x的方程$\frac{m}{x}$=kx的两个实数根分别为-2、2.
故选D.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是求出点B的坐标.本题属于基础题,难度不大,解决该题型题目时,根据正、反比例函数的对称性求出两交点的坐标是关键.

练习册系列答案
相关题目
1.下列式子中,正确的是( )
| A. | x3÷x2=x | B. | x3+x2=x5 | C. | x3-x2=x | D. | x3•x2=x6 |
18.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
17. 如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )
如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )
 如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )
如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )| A. | 12cm | B. | 9cm | C. | 7cm | D. | 15cm |
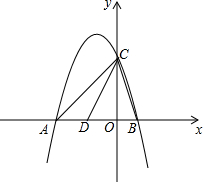 如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C. 黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).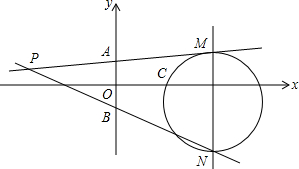 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.