题目内容
1.下列方程组用加减法求解比代入法较简便的一个是( )| A. | $\left\{\begin{array}{l}{x=2y}\\{2x+3y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-2y=6}\\{2x+y=12}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{x=6y+2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{-8x+3y=5}\\{8x+9y=1}\end{array}\right.$ |
分析 观察选项中两方程x与y的系数,利用加减消元法判断即可.
解答 解:$\left\{\begin{array}{l}{-8x+3y=5①}\\{8x+9y=1②}\end{array}\right.$,
①与②中x的系数互为相反数,故采用加减法求解比代入法较简便,
故选D
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
13.直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
| A. | x≤3 | B. | x≥3 | C. | x≥-3 | D. | x≤0 |
16.用加减法解方程组$\left\{\begin{array}{l}{2x+3y=3}\\{3x-2y=11}\end{array}\right.$时,下列四种变形中正确的是( )
| A. | $\left\{\begin{array}{l}{4x+6y=3}\\{9x-6y=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+3y=9}\\{6x-2y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x+9y=3}\\{6x-4y=11}\end{array}\right.$ |
13.某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经了解得到以下信息(如表):
(1)甲队单独完成这项工程所需天数n=35,乙队每天修路的长度m=50(米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.
| 工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
| 甲队 | 30 | n | 600 |
| 乙队 | m | n-14 | 1160 |
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.
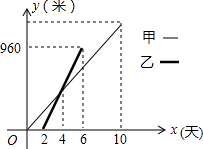 今年3月,市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A第方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:
今年3月,市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A第方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法: