题目内容
16．用加减法解方程组$\left\{\begin{array}{l}{2x+3y=3}\\{3x-2y=11}\end{array}\right.$时，下列四种变形中正确的是（ ）| A． | $\left\{\begin{array}{l}{4x+6y=3}\\{9x-6y=11}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{6x+3y=9}\\{6x-2y=22}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{6x+9y=3}\\{6x-4y=11}\end{array}\right.$ |
分析 方程组中第一个方程左右两边乘以2，第二个方程左右两边乘以3，将两方程y系数化为互为相反数，利用加减法求解即可．
解答 解：用加减法解方程组$\left\{\begin{array}{l}{2x+3y=3}\\{3x-2y=11}\end{array}\right.$时，下列四种变形中正确的是$\left\{\begin{array}{l}{4x+6y=6}\\{9x-6y=33}\end{array}\right.$，
故选C
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
8．计算：23=（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 9 |
7．下列方程中是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{3x-2y=1}\\{y=4z+1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=3}\\{2b-3a=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{\frac{1}{x}+y=3}\\{\frac{1}{y}+2x=4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{mn=-1}\\{m+n=3}\end{array}\right.$ |
4．我县万德隆商场有A、B两种商品的进价和售价如表：
已知：用2400元购进A种商品的数量与用3000元购进B种商品的数量相同．
（1）求m的值；
（2）该商场计划同时购进的A、B两种商品共200件，其中购进A种商品x件，实际进货时，生产厂家对A种商品的出厂价下调a（50＜a＜70）元出售，若商场保持同种商品的售价不变，商场售完这200件商品的总利润为y元．
①求y关于x的函数关系式；
②若限定A种商品最多购进120件最少购进100件，请你根据以上信息，设计出使该商场获得最大利润的进货方案．
| 商品 价格 | A | B |
| 进价（元/件） | m | m+20 |
| 售价（元/件） | 160 | 240 |
（1）求m的值；
（2）该商场计划同时购进的A、B两种商品共200件，其中购进A种商品x件，实际进货时，生产厂家对A种商品的出厂价下调a（50＜a＜70）元出售，若商场保持同种商品的售价不变，商场售完这200件商品的总利润为y元．
①求y关于x的函数关系式；
②若限定A种商品最多购进120件最少购进100件，请你根据以上信息，设计出使该商场获得最大利润的进货方案．
11．利用代入消元法解方程组$\left\{\begin{array}{l}{2x+3y=6①}\\{5x-3y=2②}\end{array}\right.$，下列做法正确的是（ ）
| A． | 由①得x=$\frac{6+3y}{2}$ | B． | 由①得y=$\frac{6-2x}{3}$ | C． | 由②得y=$\frac{-2+3x}{5}$ | D． | 由②得y=$\frac{5x+2}{3}$ |
1．下列方程组用加减法求解比代入法较简便的一个是（ ）
| A． | $\left\{\begin{array}{l}{x=2y}\\{2x+3y=7}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-2y=6}\\{2x+y=12}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{x=6y+2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{-8x+3y=5}\\{8x+9y=1}\end{array}\right.$ |
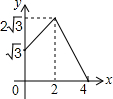
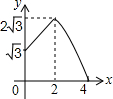
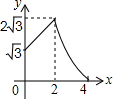
如图，平行四边形ABCD中，AB=2，BC=4，∠ABC=60°，E是BC的中点，点P、Q分别从A、E出发，沿着四边形的边向D点移动，移动时始终保持PQ∥AE，设△BPQ的面积是y，AP=x，则y关于x的函数图象大致是（ ）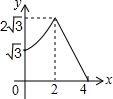
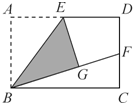如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于点F．若CF=1，FD=2，则BC的长为2$\sqrt{6}$．