题目内容
4.如果${({m-\sqrt{\frac{m}{3}}})^0}=1$,则实数m的取值范围为m>0且$m≠\frac{1}{3}$.分析 根据非零的零次幂等于1,可得答案.
解答 解:由${({m-\sqrt{\frac{m}{3}}})^0}=1$,得
m-$\sqrt{\frac{m}{3}}$≠0且m>0,
解得m>0且$m≠\frac{1}{3}$.
故答案为:m>0且$m≠\frac{1}{3}$.
点评 本题考查了零指数幂,利用非零的零次幂等于1得出不等式是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
15.下列各式经过化简后与-$\sqrt{27{x}^{3}}$不是同类二次根式的是( )
| A. | $\sqrt{27{x}^{3}}$ | B. | $\sqrt{\frac{-{x}^{3}}{27}}$ | C. | -$\frac{1}{9}$$\sqrt{3{x}^{3}}$ | D. | $\frac{\sqrt{x}}{\sqrt{3}}$ |
16.遗爱湖有5400亩,15亩=10000平方米,用科学记数法表示遗爱湖面积为( )
| A. | 8.1×105平方米 | B. | 8.1×106平方米 | C. | 3.6×105平方米 | D. | 3.6×106平方米 |
13.已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a-b为整数时,ab=( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -2 |
14.函数y=(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
| A. | m≠2 | B. | m≠-1 | C. | m=-1 | D. | m≠2且m≠-1 |
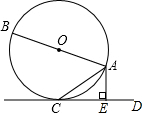 已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.
已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.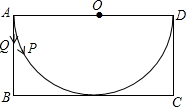 有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)
有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)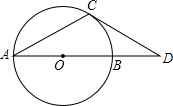 已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.
已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.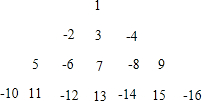 将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.
将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.