题目内容
15.下列各式经过化简后与-$\sqrt{27{x}^{3}}$不是同类二次根式的是( )| A. | $\sqrt{27{x}^{3}}$ | B. | $\sqrt{\frac{-{x}^{3}}{27}}$ | C. | -$\frac{1}{9}$$\sqrt{3{x}^{3}}$ | D. | $\frac{\sqrt{x}}{\sqrt{3}}$ |
分析 根据二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式,可得答案.
解答 解:-$\sqrt{27{x}^{3}}$=-3$\sqrt{3x}$,
A、$\sqrt{27{x}^{3}}$=3x$\sqrt{3x}$,故A是同类二次根式;
B、$\sqrt{\frac{-{x}^{3}}{27}}$=-$\frac{x\sqrt{-3x}}{9}$,故B错误;
C、C与-$\sqrt{27{x}^{3}}$是同类二次根式,故C正确;
D、$\frac{\sqrt{x}}{\sqrt{3}}$=$\frac{\sqrt{3x}}{3}$,故D正确,
故选:B.
点评 此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
10.下列函数属于反比例函数的是( )
| A. | y=$\frac{x}{5}$ | B. | y=$\frac{2}{x}$ | C. | y=x2-2x-1 | D. | y=8x-4 |
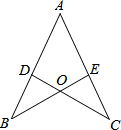 如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.
如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.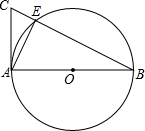 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$.