题目内容
14.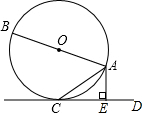 已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.
已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.
分析 连接BC,根据圆周角定理可知∠ACB=90°,再由弦切角定理得出∠ACE=∠B,故可得出△ACE∽△ABC,根据相似三角形的对应边成比例即可得出结论.
解答 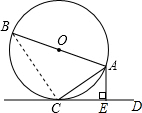 解:连接BC,
解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠ACE=∠B.
∵AE⊥CD于E,
∴∠AEC=∠ACB=90°,
∴△ACE∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AE}{AC}$,即AC2=AE•AB.
点评 本题考查的是切线的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
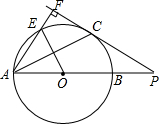 如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,
如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,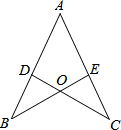 如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.
如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.