题目内容
13.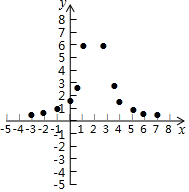 有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.小华根据学习函数的经验,对函数y=$\frac{6}{(x-2)^{2}}$的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)函数y=$\frac{6}{(x-2)^{2}}$的自变量x的取值范围是x≠2;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:函数图象关于直线x=2对称.
分析 (1)根据分式有意义的条件即可得到结论;
(2)把x=7代入y=$\frac{6}{(x-2)^{2}}$即可得到结论;
(3)根据描点法画出函数图象即可;
(4)函数图象写出该函数的一条性质即可.
解答 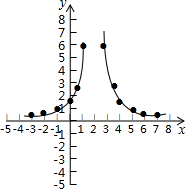 解:(1)函数y=$\frac{6}{(x-2)^{2}}$的自变量x的取值范围是x≠2,
解:(1)函数y=$\frac{6}{(x-2)^{2}}$的自变量x的取值范围是x≠2,
故答案为:x≠2;
(2)当x=7时,y=$\frac{6}{(x-2)^{2}}$=$\frac{6}{(7-2)^{2}}$=$\frac{6}{25}$;
∴m=$\frac{6}{25}$;
(3)该函数的图象如下图所示:
(4)答案不唯一,函数图象关于直线x=2对称.
故答案为:函数图象关于直线x=2对称.
点评 本题考查了二次函数的性质,反比例函数的性质,反比例函数的图象,正确的理解题意是解题的关键.

练习册系列答案
相关题目
16.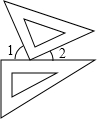 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )| A. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=90}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=180}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=180}\end{array}\right.$ |
1.m16可以写成( )
| A. | m8+m8 | B. | m8•m8 | C. | m2•m8 | D. | m4•m4 |
8.若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>$\frac{1}{2}$ | B. | k≥$\frac{1}{2}$ | C. | k>$\frac{1}{2}$且k≠1 | D. | k≥$\frac{1}{2}$且k≠1 |
5.要使二次根式$\sqrt{1-x}$有意义,则x应满足( )
| A. | x≠1 | B. | x≥1 | C. | x≤1 | D. | x<1 |
2.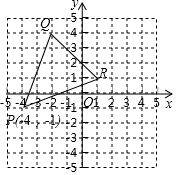 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )| A. | (-1,-3) | B. | (-2,4) | C. | (-2,-4) | D. | (2,-3) |
3.已知关于x的方程2x+4=m-x的解为非负数,则m的取值范围是( )
| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |