题目内容
17．不等式组$\left\{\begin{array}{l}x+1＞0\\ a-\frac{1}{3}x＜0\end{array}$的解集是x＞-1，则a的取值范围是a≤-$\frac{1}{3}$．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了，结合不等式组的解集即可确定a的范围．
解答 解：解不等式x+1＞0，得：x＞-1，
解不等式a-$\frac{1}{3}$x＜0，得：x＞3a，
∵不等式组的解集为x＞-1，
则3a≤-1，
∴a≤-$\frac{1}{3}$，
故答案为：a≤-$\frac{1}{3}$．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．作为世界文化遗产的长城，其总长大约为6700000m．将6700000用科学记数法表示为（ ）
| A． | 6.7×105 | B． | 6.7×106 | C． | 0.67×107 | D． | 67×108 |
5．一天时间为86400秒，用科学记数法表示这一数字是（ ）
| A． | 864×102 | B． | 86.4×103 | C． | 8.64×104 | D． | 0.864×105 |
12．
如图，大小不同的两个磁块，其截面都是等边三角形，小三角形边长是大三角形边长的一半，点O是小三角形的内心，现将小三角形沿着大三角形的边缘顺时针滚动，当由①位置滚动到④位置时，线段OA绕点O顺时针转过的角度是（ ）
如图，大小不同的两个磁块，其截面都是等边三角形，小三角形边长是大三角形边长的一半，点O是小三角形的内心，现将小三角形沿着大三角形的边缘顺时针滚动，当由①位置滚动到④位置时，线段OA绕点O顺时针转过的角度是（ ）| A． | 240° | B． | 360° | C． | 480° | D． | 540° |
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
9．在《数据分析》章节测试中，“勇往直前”学习小组7位同学的成绩分别是92，88，95，93，96，95，94．这组数据的中位数和众数分别是（ ）
| A． | 94，94 | B． | 94，95 | C． | 93，95 | D． | 93，96 |
13．
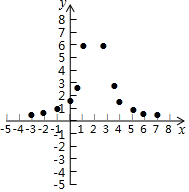有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．
小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．
有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．