题目内容
3.已知关于x的方程2x+4=m-x的解为非负数,则m的取值范围是( )| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |
分析 先求出方程的解,根据题意得出不等式,求出不等式的解集即可.
解答 解:解方程2x+4=m-x得:x=$\frac{m-4}{3}$,
∵方程2x+4=m-x的解为非负数,
∴$\frac{m-4}{3}$≥0,
解得:m≥4,
故选B.
点评 本题考查了解一元一次方程,一元一次方程的解,解一元一次不等式等知识点,能得出关于m的不等式是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.
小华根据学习函数的经验,对函数y=$\frac{6}{(x-2)^{2}}$的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)函数y=$\frac{6}{(x-2)^{2}}$的自变量x的取值范围是x≠2;
(2)下表是y与x的几组对应值.
求m的值;
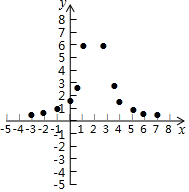
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:函数图象关于直线x=2对称.
 有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.小华根据学习函数的经验,对函数y=$\frac{6}{(x-2)^{2}}$的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)函数y=$\frac{6}{(x-2)^{2}}$的自变量x的取值范围是x≠2;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:函数图象关于直线x=2对称.
18.计算3-2的结果是( )
| A. | -6 | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
15.下列说法中错误的是( )
| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线相等的菱形是正方形 | |
| C. | 两条对角线互相垂直的矩形是正方形 | |
| D. | 两条对角线相等的四边形是矩形 |
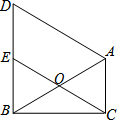 如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.
如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D. 如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.
如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.